Minkowski addition

According to wikipedia the Minkowski sum of two sets of vectors $A$ and $B$ in Euclidean space is formed by adding each vector in $A$ to each vector in $B$.

$$A+B=\{\mathbf {a} +\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}$$

All images come from an implementation of Minkowski Addition/Difference in the C# Script component for Grasshopper/Rhino3d.

Minkowski Addition (yellow polygon) of white polygon $A$ with red polygon $B$: $A{\oplus}B$

The Minkowski difference is defined as:

$$A+B=\{\mathbf {a} +\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}$$

Minkowski Difference (yellow polygon) of white polygon $A$ with red polygon $B$: $A{\oplus}-B$

Why do we care?
The Minkowski difference gives us all the possible vectors where we can place a polygon close to another without overlaps. This means that we can restrict the search space for a brute-force algorithm for packing from exhausting every polygon $n$ to every other polygon $m$ to every degree of freedom $xy$: $\mathcal{O}(n^{m^{x^{y}}})$ to every polygon $n$ with every other polygon $m$ to every possible vector obtained from the Minkownski difference $v:$ $\mathcal{O}(n^{m^{v}})$. Although the algorithmic complexity does not seem to improve much, remember that when we are dealing with $x^{y}$ the permutations differ by orders of magnitude, suppose we have a search space $-5.00\leq{x}\leq{5.00}$ and $-5.00\leq{y}\leq{5.00}$ that means that we are iterating $10^{10^{10}}=1\text{e+}100$ ($10$ from the fractional tenths $10$ from the fractional hundredths and $10$ from the range of the search space) by $1\text{e+}100$ ($x$ and $y$ are equal as they have the same range and fractional parts), so $1\text{e+}100^{1\text{e+}100}$ permutations, compared to $d=n+m$ where $n$ is the number of points of Polygon A and $m$ is the number of points of Polygon B.
*Note we are dealing only with 2D (with no rotations) and that for packing, simulated annealing or other heuristics are preferred over the brute-force approach.
Minkowski sums are also used in robot planning and videogames, as the Minkowski difference can be used to test for collisions.

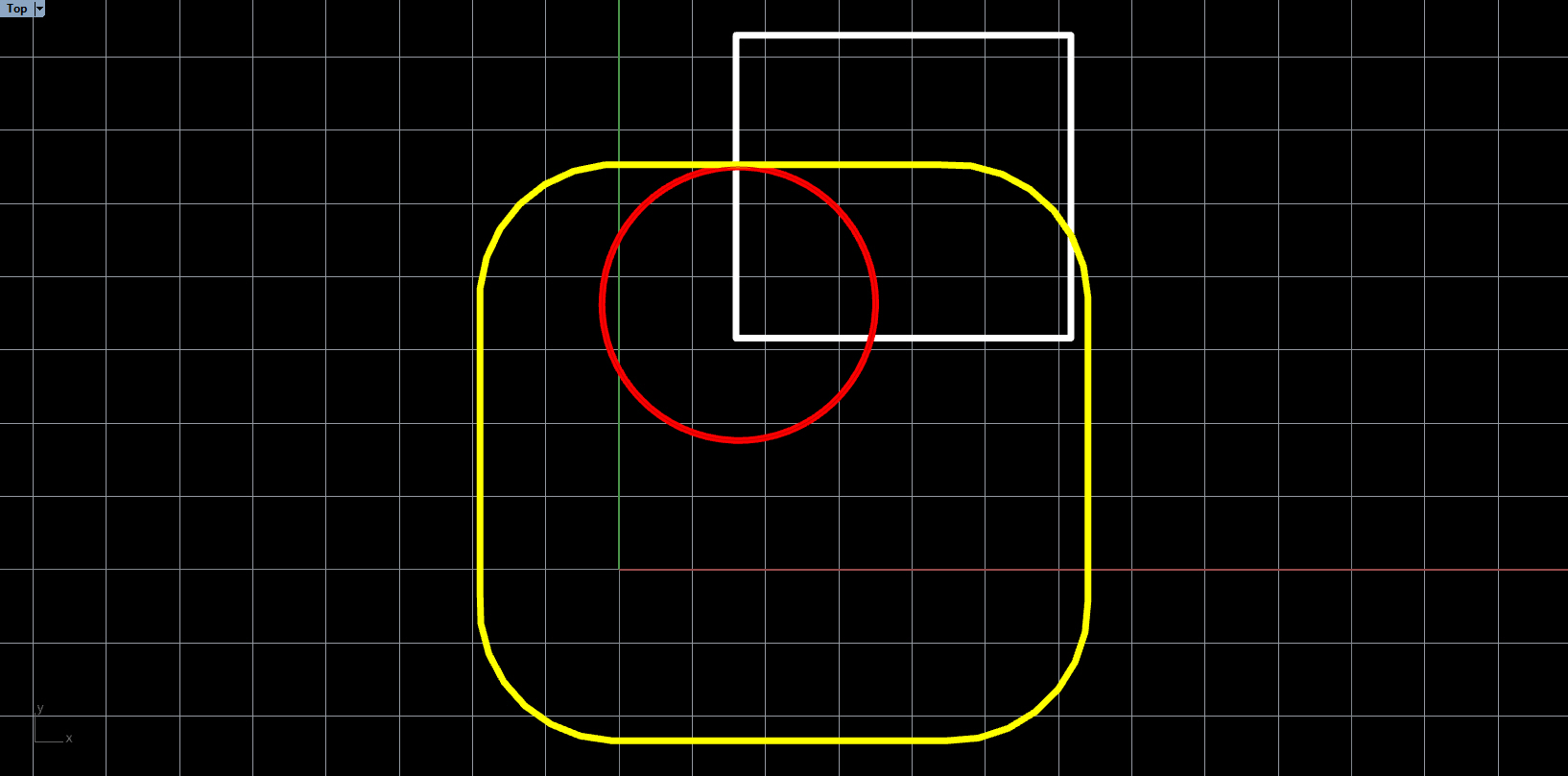
Polygon A and Polygon B intersect, we can tell so because the origin is contained in the Minkowski difference

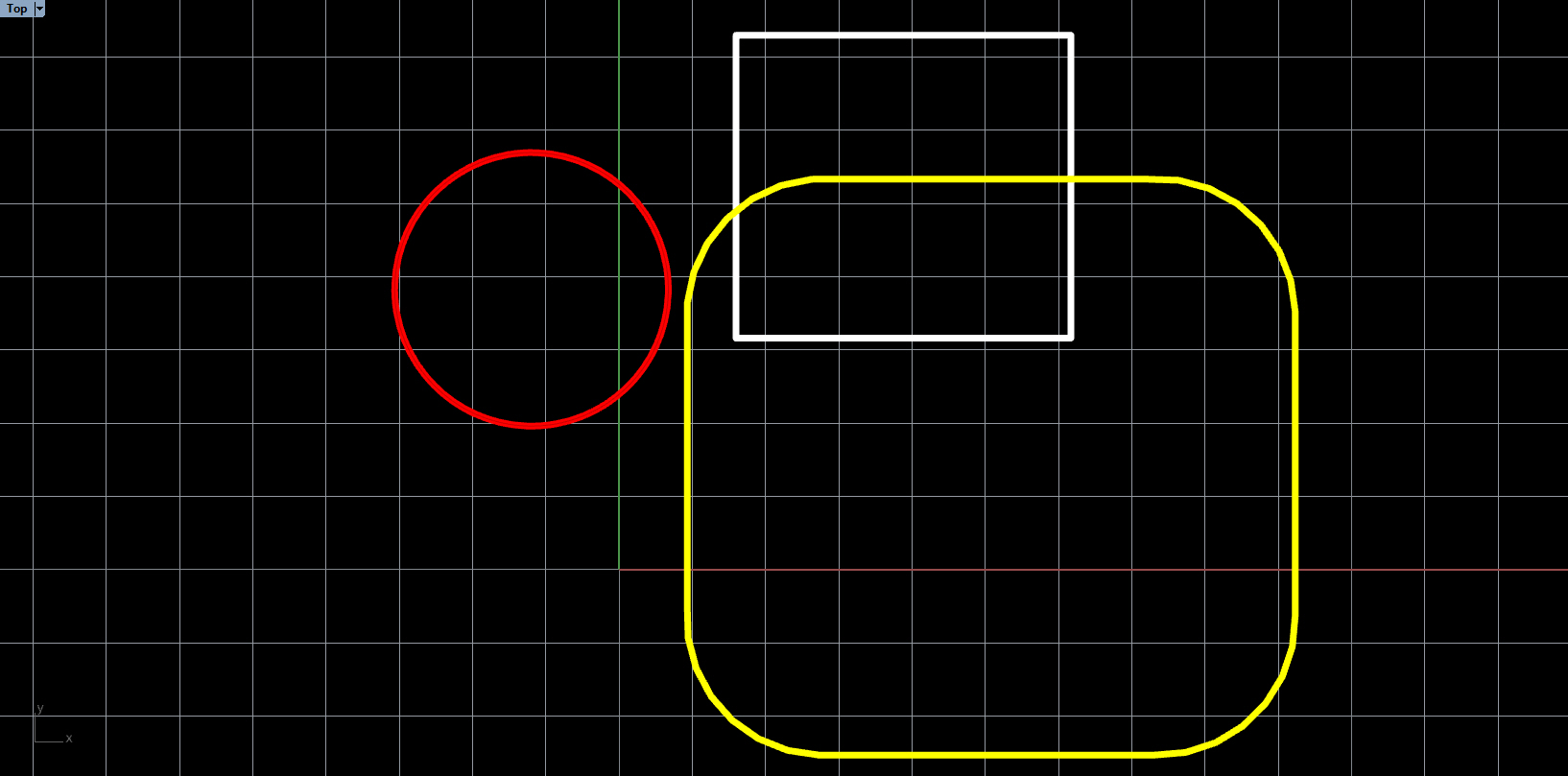
Polygon A and Polygon B do not intersect, we can tell so because the origin is not contained in the Minkowski difference