Nesting/Packing

A common problem in computational design is that the model must be discretized into pieces that can be cut and assembled, once this pieces have been derived from the computer model, the designer has to place the pieces in a way that reduces the amount of "sheet" material from which the CNC is cutting the pieces, doing this manually is tedious and can often lead to non-optimal placements. This kind of problem can be solved by a Nesting algorithm. Due to the industrial nature of the problem, there are many papers that propose heuristics that improve the brute force approach of testing every polygon against every polygon against the sheet.

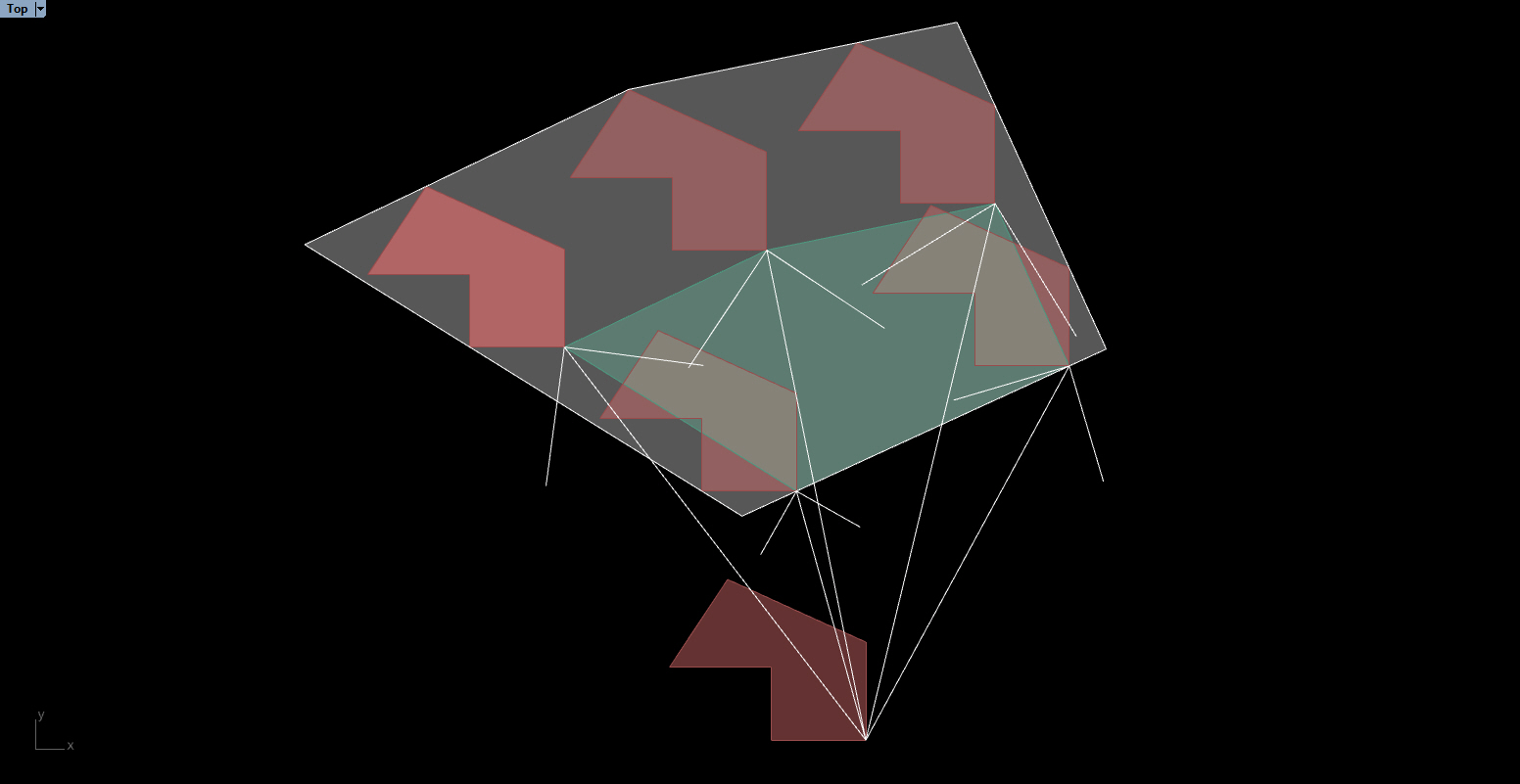
All images and videos come from an implementation of a custom coded nesting algorithm for Grasshopper/Rhino3d.

The transparent white polygon is the "sheet", the inner coloured polygons are packed/nested inside the sheet. The sheet is usually rectangular, but as other objects are cutted from the original rectangle, the shape of the sheet can end up having a non-orthogonal shape like this one.

For the first placemenent we need to introduce the concept of the InnerFitPolygon IFP:

The

Why do we care?
The Minkowski difference gives us all the possible vectors where we can place a polygon close to another without overlaps. This means that we can restrict the search space for a brute-force algorithm for packing from exhausting every polygon $n$ to every other polygon $m$ to every degree of freedom $xy$: $\mathcal{O}(n^{m^{x^{y}}})$ to every polygon $n$ with every other polygon $m$ to every possible vector obtained from the Minkownski difference $v:$ $\mathcal{O}(n^{m^{v}})$. Although the algorithmic complexity does not seem to improve much, remember that when we are dealing with $x^{y}$ the permutations differ by orders of magnitude, suppose we have a search space $-5.00\leq{x}\leq{5.00}$ and $-5.00\leq{y}\leq{5.00}$ that means that we are iterating $10^{10^{10}}=1\text{e+}100$ ($10$ from the fractional tenths $10$ from the fractional hundredths and $10$ from the range of the search space) by $1\text{e+}100$ ($x$ and $y$ are equal as they have the same range and fractional parts), so $1\text{e+}100^{1\text{e+}100}$ permutations, compared to $d=n+m$ where $n$ is the number of points of Polygon A and $m$ is the number of points of Polygon B.
*Note we are dealing only with 2D and that for packing, simulated annealing or other heuristics are preferred over the brute-force approach.
Minkowski sums are also used in robot planning and videogames, as the Minkowski difference can be used to test for collisions.

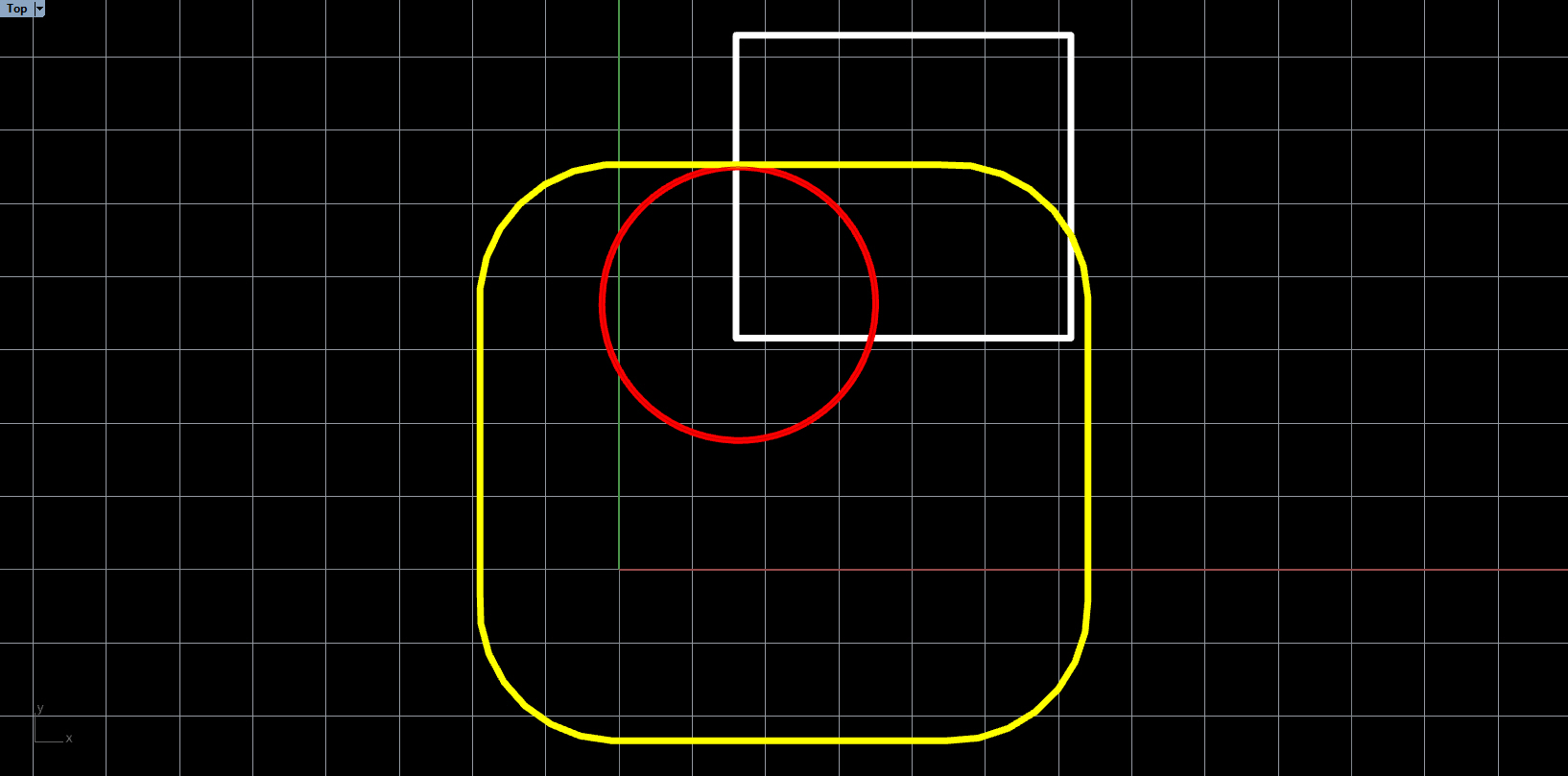
Polygon A and Polygon B intersect, we can tell so because the origin is contained in the Minkowski difference

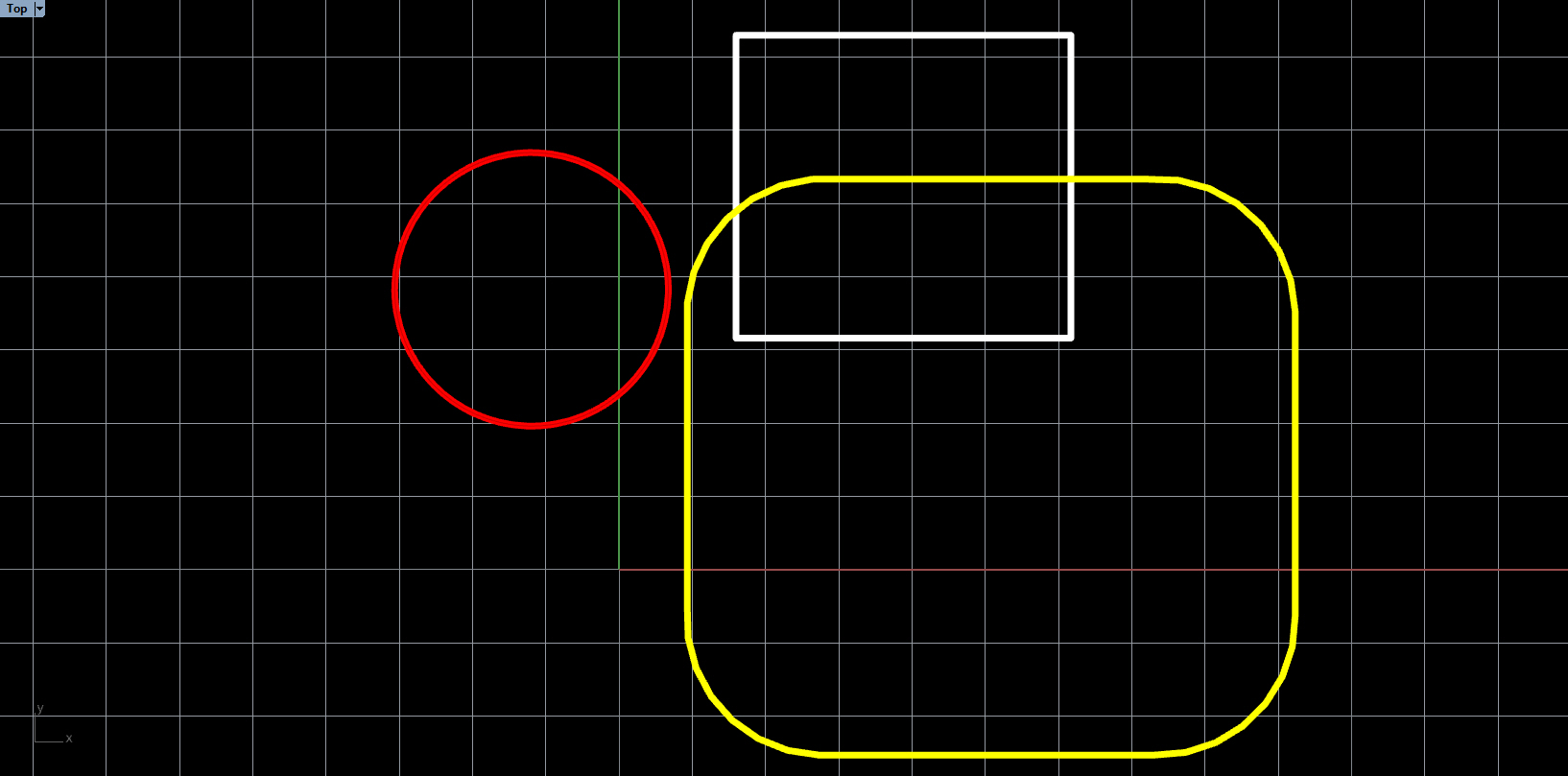
Polygon A and Polygon B do not intersect, we can tell so because the origin is not contained in the Minkowski difference